How TRM Recursive Reasoning Proves Less is More

Do you think that a small neural network (like TRM) can outperform models many times larger in reasoning tasks? How is it possible for billions of LLM parameters to have such a small number of modest million-parameter iterations solving puzzles?

“Currently, we live in a scale-obsessed world: More data. More GPUs mean bigger and better models. This mantra has driven progress in AI till now.”

But sometimes less really is more, and the Ting Recursive Models (TRMs) are bold examples of this phenomenon. The results, as proven within this report, are powerful: TRMs achieve 87.4% accuracy on Sudoku-Extreme and 45% on ARC-AGI-1, while exceeding the performance of larger hierarchical models, and while some state-of-the-art models like DeepSeek R1, Claude, and o3-mini scored 0% on Sudoku. And DeepSeek R1 got 15.8% on ARC-1 and only 1.3% on ARC-2, while a TRM 7M model scores 44.6% accuracy. In this blog, we’ll discuss how TRMs achieve maximal reasoning through minimal architecture.

The Quest for Smarter, Not Bigger, Models

Artificial intelligence has transitioned into a phase dominated by gigantic models. The movement has been a straightforward one: just scale everything, i.e., data, parameters, computation, and intelligence will emerge.

However, as researchers and practitioners persist in expanding that boundary, a realization is setting in. Bigger doesn’t always equal better. For structured reasoning, accuracy, and stepwise logic, larger language models often fail. The future of AI may not reside in how big we can build, but rather how intelligent we can think. Therefore, it encounters 2 major issues:

The Problem with Scaling Large Language Models

Large Language Models have transformed natural language understanding, summarization, and creative text generation. They can seemingly detect patterns in the text and produce human-like fluency.

Nonetheless, when they are prompted to engage in logical reasoning to solve Sudoku puzzles or map out mazes, the genius of those same models diminishes. LLMs can predict the next word, but that does not imply that they can reason out the next logical step. When engaging with puzzles like Sudoku, a single misplaced digit invalidates the entire grid.

When Complexity Becomes a Barrier

Underlying this inefficiency is the one-sided, i.e., similar architecture of LLMs; once a token is generated, it is fixed as there is no capacity to fix a misstep. A simple logical mistake early on can spoil the entire generation, just as one incorrect Sudoku cell ruins the puzzle. Thus, scaling up will not ensure stability or improved reasoning.

The enormous computing and data requirements make it nearly impossible for most researchers to access these models. Thus, there lies within this a paradox where some of the most powerful AI systems can write essays and paint pictures but are incapable of accomplishing tasks that even a rudimentary recursive model can easily solve.

The issue is not about data or scale; rather, it is about inefficiency in architecture, and that recursive intellectualism may be more meaningful than expansive intellect.

Hierarchical Reasoning Models (HRM): A Step Toward Simulated Thinking

The Hierarchical Reasoning Model (HRM) is a recent advancement that demonstrated how small networks can solve complex problems through recursive processing. HRM has two transformer implementations, one low-level net (f_L) and one high-level net (f_H). Each pass runs as follows: the f_L takes the input question and the current answer, plus the latent state, while the f_H updates the answer based on the latent state. This is kind of a hierarchy of fast ”thinking” (f_L), and slower ”conceptual” shifts (f_H). Both f_L and f_H are four-layer transformers with ~27M parameters in total.

HRM’s architecture trains with deep supervision: during training, HRM runs up to 16 successive generation “improvement steps” and computes a loss for the answer each time, and compares the gradients from all the previous steps. This essentially mimics a very deep network, but eliminates full backpropagation.

The model has an adaptive halting (Q-learning) signal that will decide the next time when the model will train and when to stop updating on each question. With this complicated methodology, HRM performed very well: it outperformed large LLMs on Sudoku, Maze, and ARC-AGI puzzles with only a small sample with supervised learning.

In other words, HRM demonstrated that small models with recursion can perform comparably or better than much larger models. However, HRM’s framework is based on multiple strong assumptions. Its benefits arise primarily from high supervision, not the recursive dual network.

In reality, there is no certainty that f_L and f_H reach an equilibrium in a few steps. HRM also adopts a two-network type of architecture based on biological metaphors, making the architecture difficult to understand and tune. Finally, HRM’s adaptive halting increases the training speed but doubles the computation.

Tiny Recursive Models (TRM): Redefining Simplicity in Reasoning

Tiny Recursive Models (TRMs) streamline the recursive process of HRMs, replacing the hierarchy of two networks with a single tiny network. Given a complete recursion process, a TRM performs this process iteratively and backpropagates through the entire final recursion without needing to impose the fixed-point assumption. The TRM explicitly maintains a proposed solution 𝑦 and a latent reasoning state 𝑧 and iterates over merely updating 𝑦 and the 𝑧 reasoning state.

In contrast to the sequential HRM instance, the fully compact loop is able to take advantage of massive gains in generalization while reducing model parameters in the TRM architecture. The TRM architecture essentially removes dependence on a fixed point and IFT(Implicit Fixed-point Training) altogether, as PPC(Parallel Predictive Coding) is used for the full recursion process, just like HRM models. A single tiny network replaces the two networks in the HRM, which lowers the number of parameters and minimizes the risk of overfitting.

How TRM Outperforms Bigger Models

TRM keeps two distinct variable states, the solution hypothesis 𝑦, and the latent chain-of-thought variable 𝑧. By keeping 𝑦 separate, the latent state 𝑧 does not have to persist both the reasoning and the explicit solution. The primary benefit of this is that the dual variable states mean that a single network can perform both functions, iterating on 𝑧 and converting 𝑧 into 𝑦 when the inputs differ only by the presence or absence of 𝑥.

By removing a network, the parameters are cut in half from HRM, and model accuracy in key tasks increases. The change in architecture allows the model to concentrate its learning on the effective iteration and reduces the model capacity where osmosis would have overfitted. The empirical results demonstrate that the TRM improves generalization with fewer parameters. Hence, the TRM found that fewer layers provided better generalization than having more layers. Reducing the number of layers to two, where the recursion steps that were proportional to the depth yielded better results.

The model is deep supervised to improve $y$ to the truth at training time, at every step. It is designed in such a way that even a couple of gradient-free passes will get $(y,z)$ closer to a solution – thus learning how to improve the answer only requires one full gradient pass.

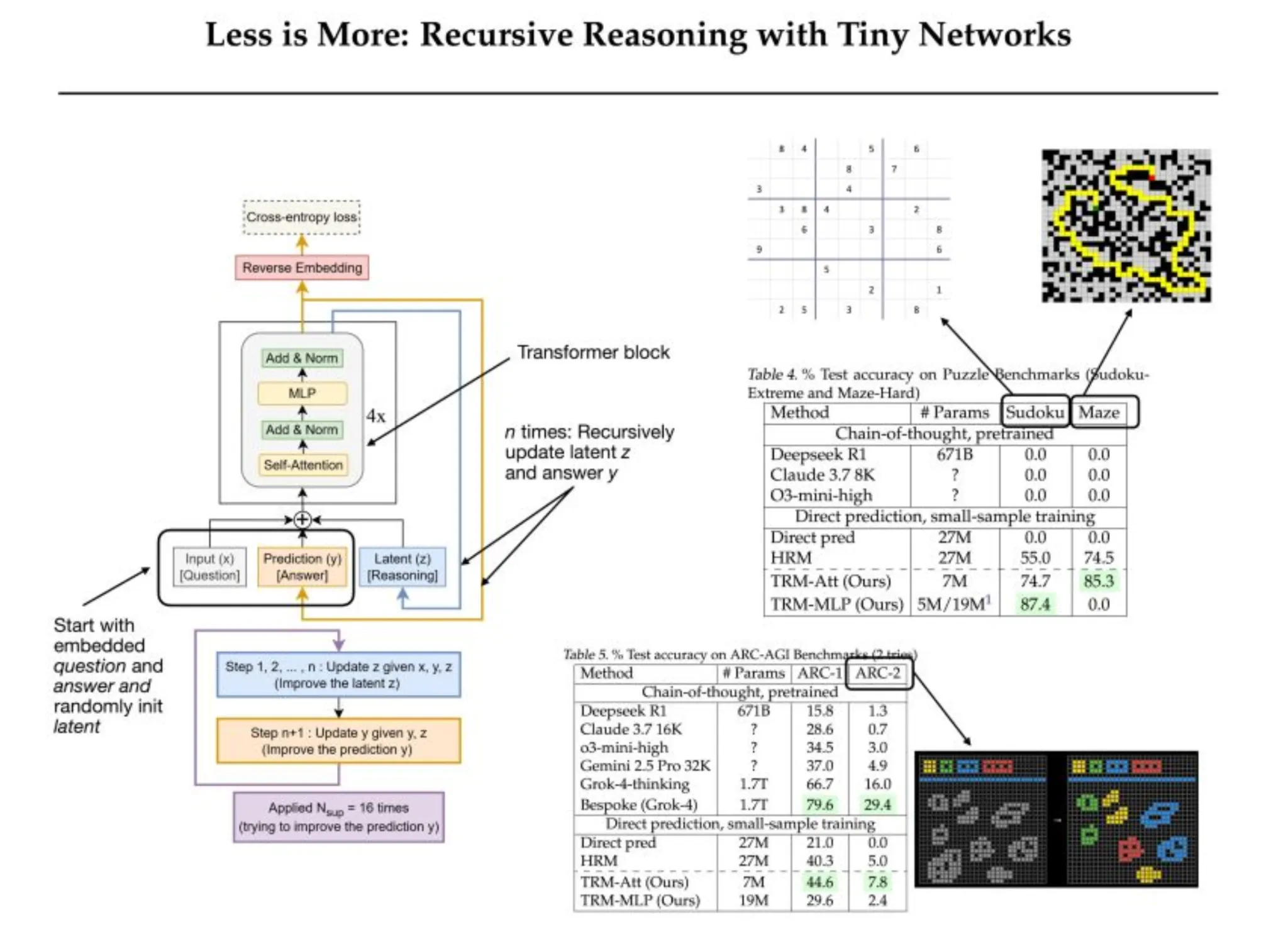
Benefits of TRM

This design is streamlined and has many benefits:

• No Fixed-Point Assumptions: TRM eliminates fixed-point dependencies and backpropagates through every recursion. Running a series of no-gradient recursions.
• Simpler Latent Interpretation: TRM defines two state variables: y (the solution) and z (the memory of reasoning). It alternates between refining both, which captures the thought for one end and the output for another. Using exactly these two, neither more nor less than two, was undoubtedly optimal to maintain clarity of logic while increasing the performance of reasoning.
• Single Network, Fewer Layers (Less Is More): Instead of using two networks, as the HRM model does with f_L and f_H, TRM compacts everything into one single 2-layer model. This reduces the number of parameters to approximately 7 million, circumvents overfitting, and boosts accuracy overall for Sudoku from 79.5% to 87.4%.
• Task-Specific Architectures: TRM is designed to adapt the architecture to each case task. Instead of using two networks, as the HRM model does with f_L and f_H, TRM compacts everything into one single 2-layer model. This reduces the number of parameters to approximately 7 million, circumvents overfitting, and boosts accuracy overall for Sudoku from 79.5% to 87.4%.
• Optimized Recursion Depth: TRM also employs an Exponential Moving Average (EMA) on the weights to stabilize the network. Smoothing weights helps reduce overfitting on small data and stability with EMA.

Experimental Results: Tiny Model, Big Impact

Tiny Recursive Models demonstrate that small models can outperform large LLMs on some reasoning tasks. On several tasks, TRM’s accuracy exceeded that of HRM and large pre-trained models:

• Sudoku-Extreme: These are very hard Sudokus. HRM (27M params) is 55.0% accurate. TRM (only 5–7M params) jumps to 87.4 (with MLP) or 74.7 (with attention). No LLM is close at all. The state-of-the-art chain-of-thought LLMs (Deepseek R1, Claude, o3-mini) scored 0% on this dataset.
• Maze-Hard: For pathfinding mazes with solution length >110, TRM w/ attention is 85.3% accurate versus HRM’s 74.5%. The MLP version got 0% here, indicating self-attention is necessary. Again, trained LLMs got ~0% on Maze-Hard in this small-data regime.
• ARC-AGI-1 & ARC-AGI-2: On ARC-AGI-1, TRM (7M) got 44.6% accuracy vs HRM 40.3%. On ARC-AGI-2, TRM scored 7.8% accuracy versus HRM’s 5.0%. Both models do well versus a direct prediction model, which is a 27M model (21.0% on ARC-1 and a fresh LLM chain-of-thought Deepseek R1 got 15.8% on ARC-1 and 1.3% on ARC-2). Even on heavy test time compute, the top LLM Gemini 2.5 Pro only got 4.9% on ARC-2 while the TRM got double that (virtually no fine-tuning data).

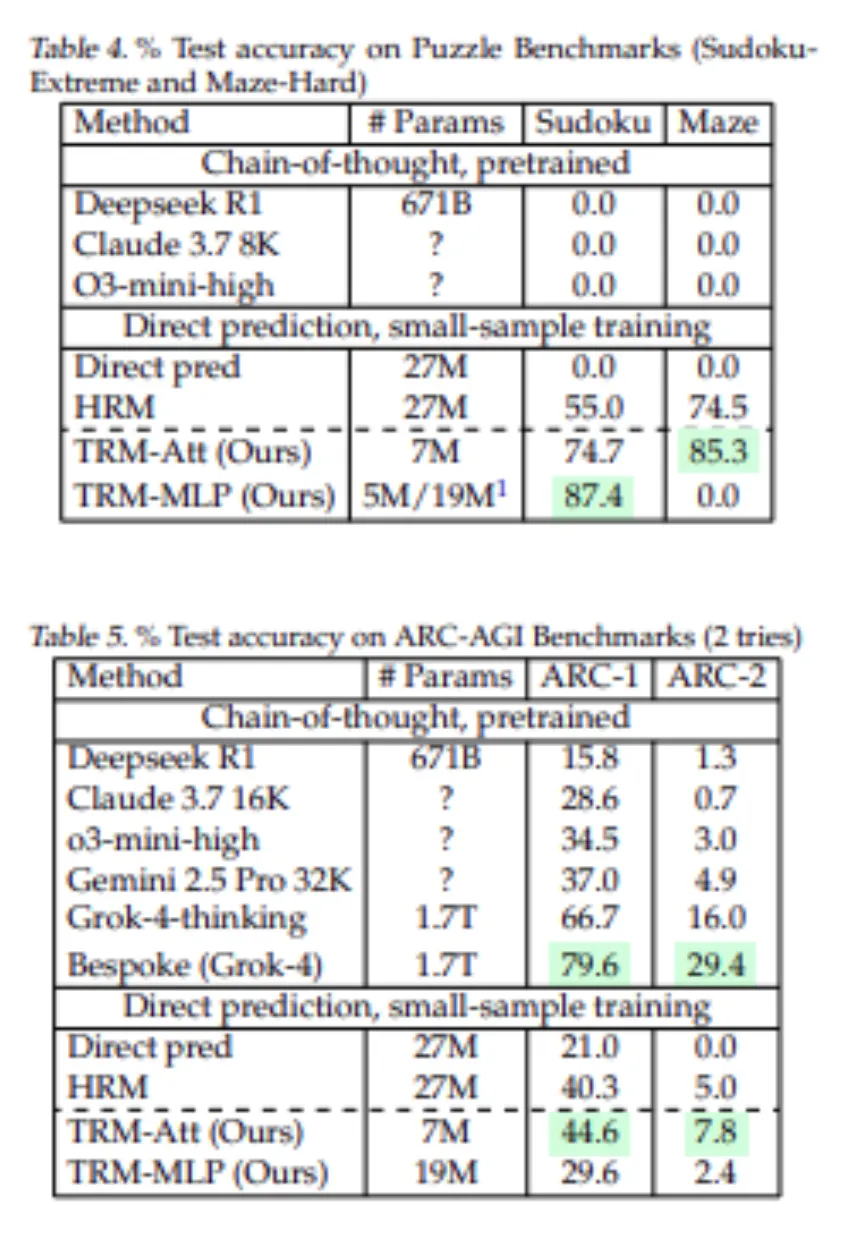
Conclusion

Tiny Recursive Models illustrate how you can achieve considerable reasoning abilities with small, recursive architectures. The complexities are stripped away (i.e., there is no fixed-point trick/use of dual networks, no dense layers). TRM gives more accurate results and uses fewer parameters. It uses half the layers and condenses two networks and only has some simple mechanisms (EMA and a more efficient halting mechanism).

Essentially, TRM is simpler than HRM, yet generalizes much better. This paper shows that well-designed small networks with recursive, deep, and supervised learning can successfully perform reasoning on hard problems without going to a massive size.

Nonetheless, the authors do pose some open questions for consideration, for example, why exactly does recursion help so much more? Why not just make a bigger feedforward net, for example?

For now, TRM is a powerful example of efficient AI architectures in that small networks outperformed LLMs on logic puzzles and demonstrates that sometimes less is more in deep learning.

Hello! I’m Vipin, a passionate data science and machine learning enthusiast with a strong foundation in data analysis, machine learning algorithms, and programming. I have hands-on experience in building models, managing messy data, and solving real-world problems. My goal is to apply data-driven insights to create practical solutions that drive results. I’m eager to contribute my skills in a collaborative environment while continuing to learn and grow in the fields of Data Science, Machine Learning, and NLP.